RESEARCH
形が生まれる原理を見出だす
自然界のさまざまな生きものが見せる樹状パターンには、領域を一様に覆いながら成長していく共通性が見られます。そこにはたらく原理を、数理モデルを用いることで明らかにしていきます。
1.さまざまな生きものが見せる樹状パターン
生きものの体づくり、つまり発生過程では、たった一つの細胞である受精卵が、細胞分裂と細胞分化を繰り返し、組織をつくっていく。ここで細胞や組織が獲得する形には、それぞれ生体機能における重要な役割がある。発生の初期における組織や細胞の一様で等方的な性質(註1)が壊れ、構造を作る過程が、何度もくり返されることで個体の形がつくり出される。
最近になって形態形成現象のいくつかは、数理科学や物理学で解き明かせることが分かってきた。生きもののつくる形態の典型例として樹状パターンがある(図1)。葉脈や樹木の枝、神経細胞のつくる樹状突起、血管や肺の樹状パターンは馴染み深い例と言ってよいだろう。これらの樹状パターンには、それぞれに機能的な意味がある。
実は、樹状パターン形成の先駆的な研究として、10年ほど前、バクテリアが培養条件によっては枝分かれをしたコロニーをつくることも見出だされている。これらの樹状パターンは、共通した原理に支配されている可能性があると考えてもよさそうだ。
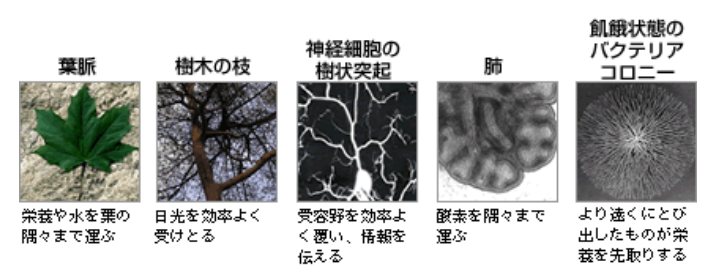
(図1) 生きものによる樹状パターン
効率よく領域を覆い、さまざまなはたらきを生む。
(註1) 等方的な性質
物質の物理的性質が方向によって異ならない性質をさす。
2.領域を効率よく埋める神経細胞
そこで、神経細胞の形態形成について、私が京都大学大学院生命科学研究科の上村匡教授、杉村薫研究員(現、理化学研究所)と共同で行った研究を紹介しよう。神経細胞は、入力を受けもつ樹状突起と出力用の突起である軸索をもつ(図2)。
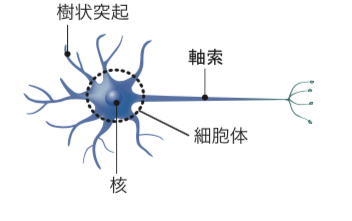
(図2) 神経細胞
入力を受け持つ樹状突起と出力用の突起(軸索)、核を持つ細胞体からなる。軸索の末端は、他の神経細胞の樹状突起や骨格筋細胞などと接しており、興奮を伝達する。
樹状突起の樹状パターンは、神経細胞の種類ごとに多様なのだが、その中でも空間的に非常に秩序だったパターンを示すものがある。ショウジョウバエの表皮下に存在する神経細胞(daニューロン(註2))の樹状突起は、胚の表皮を隅々までむらなく覆い、同じ細胞体由来のものも、異なる細胞体由来のものも、互いに重ならない性質をもつ。とくに、異なる細胞体由来の樹状突起が重ならない性質によって、神経細胞は、効率よく表皮領域を分割して分布している(図3)。これをタイリングと呼ぶ。このタイリングによって、樹状突起が表皮上にむらなく分布しているので、表皮からの入力が一様に伝わるのである。
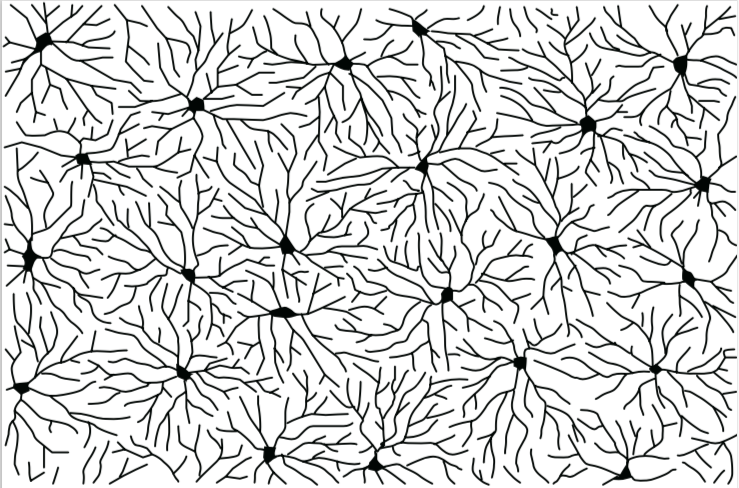
(図3) 神経細胞の分布の様子
神経細胞の樹状突起は互いにほとんど重複せず、領域全体を覆っている。
空間をむらなく覆う性質がどのように制御されているかは、再生実験によって顕著に示される。daニューロンの樹状突起の分岐近くを比較的若い段階で切断したところ、23時間後には新たな突起の再生が見られた(図4)。興味深いことに、新たな突起は切断された所から再生せずに、細胞体からより遠い位置から分岐し、回りこむようにして空白領域を埋めた。
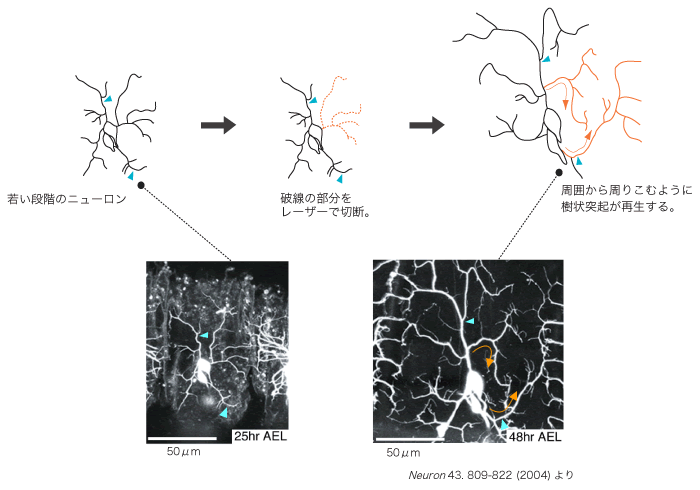
(図4) 樹状突起の切断実験
若い段階のニューロンの樹状突起を根元からレーザーで切断すると、23時間後には周囲から周りこむように樹状突起が再生する。
(註2) da neuron(dendric arborization (da) neuron)
ショウジョウバエの胚後期で誕生し、胚期~幼虫期に樹状突起を発達させる。表皮組織と筋肉組織の間にシート状に張り巡らされている。
3.樹状パターンを生み出すモデルをつくる
樹状突起が形成されるメカニズムは、未だ明らかになっていない。しかし抽象的なモデルにより、秩序形成の原理を理解することが可能である。我々が、作った「Cell compartmentモデル」を紹介しよう。
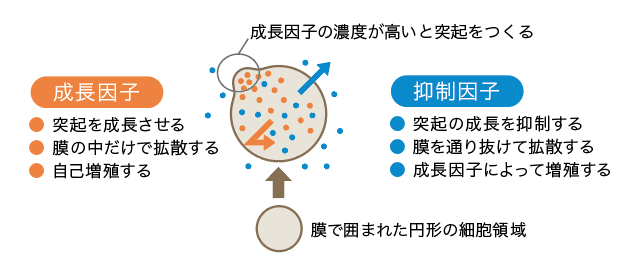
(図5) 神経細胞のCell compartmentモデル
細胞領域の成長を制御する二つの拡散性の因子が存在すると仮定している。
このモデルでは、まず二次元空間に円形の細胞領域を仮定し(図5)、細胞領域はダイナミックに変形できるとする。次に、細胞領域内だけを自由に拡散できる成長因子を仮定する。成長因子の濃度がある閾値以上高くなると、その部分の細胞領域は伸長し、突起となる。一方、突起の成長を押さえる抑制因子を仮定する。これは成長因子に伴って合成され、細胞の内外を自由に拡散できる因子だとする。成長因子と抑制因子との間には、多くの生物パターンに対して用いられる反応拡散方程式モデルの一種、活性因子・抑制因子モデルの相互作用関係(註3)が働くとする。成長因子は自己触媒的に増える一方で抑制因子をつくり出し、抑制因子の濃度が高くなると成長因子の増殖が抑えられる。
このような設定をしたCell compartmentモデルは、二種類のフィードバック、すなわち成長因子と細胞領域との間の空間的なフィードバックと、成長因子と抑制因子との間の化学的なフィードバックを含んでいる。このモデルにより二つの性質が生まれる。第一にわずかな凹凸の変化を拡大し、枝分かれへと発展させる性質、第二に近接する樹状突起が互いの成長を抑制し合うという性質である。
(註3) 活性因子-抑制因子の相互作用関係
数学者アラン・チューリングが発見した、簡単な化学反応と拡散により自律的にパターンが形成される原理、「チューリングの拡散不安定性」に基づく化学反応のモデルの一つ。活性因子と抑制因子という二つの分子の相互作用を指す。これらの因子の相互作用によって、動物の皮膚の模様などがつくられることが知られている。
[関連記事]
季刊生命誌11号「チューリングの卵 - 生物の模様の秘密」近藤 滋
4.わずかな凹凸が拡大されて樹状パターンへ
このモデルに基づき、成長因子と抑制因子の濃度変化が引き起こす細胞領域の変化を数値計算で出した(図6)。初期状態の細胞の形は円形で等方的であるが、このシステムは自ら等方性を破壊し、枝分かれをつくりだす。枝の伸長と分岐が次々とくり返され、全体として樹状パターンが形成されるのである。分岐してから次の枝へと分岐するまでの長さはばらついており、個々の分岐は局所的な振る舞いのように見えるが、出来上がったパターンを見ると、ほぼ一様に枝が分布している。
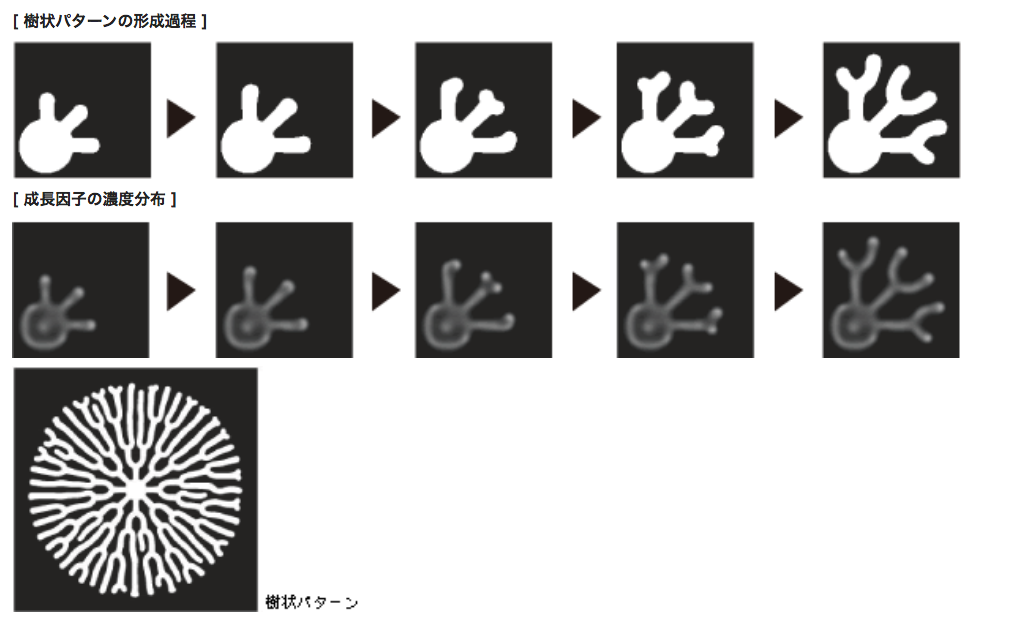
(図6) Cell compartmentモデルによる樹状パターンの再現
個々の突起が伸長と分岐を繰り返すことで、全体としてほぼ一様に枝が分布する樹状パターンが形成される。
突起の先端付近は、成長因子の濃度が高くなっている。
このような樹状パターンはどのようにしてできるのだろう。このモデルでは、細胞領域の境界のわずかな凹凸が拡大されることで突起へと発展する過程がくり返される。この過程は、「飛び出した場所が、より成長しやすくなる」という性質を考えると理解できる。
わずかなゆらぎによって、細胞領域の境界付近で、たまたま突出した所ができたとする(図7)。突起の先端付近では、活性因子の濃度が高い状態になっているが、同時に抑制因子も高濃度で存在している。抑制因子は細胞内外を自由に出入りできるため、活性因子よりも拡散係数(註4)が大きくなる。そこで抑制因子の濃度勾配は、樹状突起の凹凸よりもゆるやかなので、わずかに突出した所は、周囲に比べて抑制因子の効果を受けにくい。そのため、飛び出した所の成長速度は周囲よりも速くなる。この過程がくり返されると、樹状パターンがつくられるのだ。
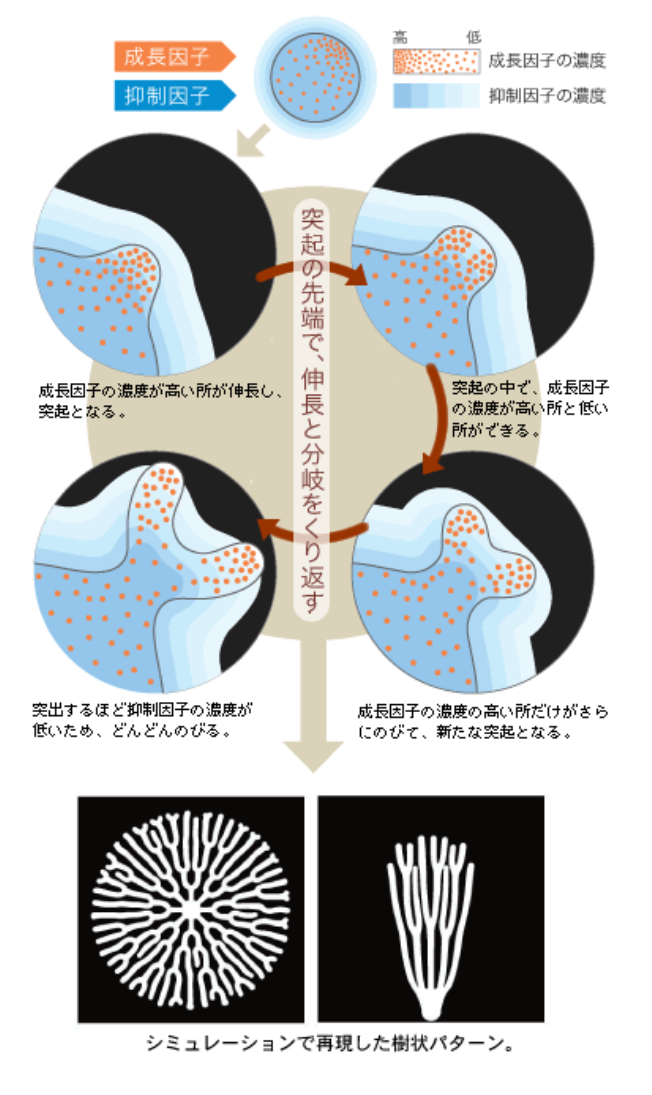
(図7) 樹状パターンが生まれるしくみ
二つの拡散因子の濃度勾配の差によって、わずかな凹凸が拡大され、突起先端で伸長と分岐がくり返される。
このモデルは、単に現実の神経細胞と似たパターンをつくるだけでなく、神経細胞に特徴的な空間制御である領域を分割する性質(タイリング)も見せた。図8は、初期条件として複数の細胞体を与えたときに得られたパターンであり、伸長した突起が他の細胞体由来の樹状突起に近づいたところで、樹状突起の成長が止まっている。これは、隣接する細胞体由来の突起が抑制因子を放出し、互いに成長を抑制し合っているからだと説明できる。
また計算機シミュレーションの場合に、成長途中の突起の一部を削除すると、実験による再生とほぼ同じ振る舞いが見られた。すなわち、切除された箇所ではなく、より遠い位置から新たな突起が形成され、それらが回りこむようにして、空いた空間を充填する。この現象も私たちのモデルで矛盾なく説明できる。突起の一部を削除した場合、そこには抑制因子が高濃度で残っているので、切断箇所はこれ以上成長できない。そこで、周囲の突起が有利になり、それが空いているところへ回りこむように伸びるのだ。
(図8) タイリングの様子
初期条件として複数の細胞体を与えると、互いの枝が重複しない空間分割が再現された。
(註4) 拡散係数
ある因子が周囲に拡散する場合、その広がり度合いを示す数値のこと
5.成長因子の分布を予測する
樹状突起の形態をよく観察すると、樹状突起がきちんと整列された滑らかなものと、乱れたものがあることに気づく。計算機シミュレーションで成長因子と抑制因子の合成速度を変えたところ、滑らかなパターンから、やや乱れたパターンが出来上がった(図9)。
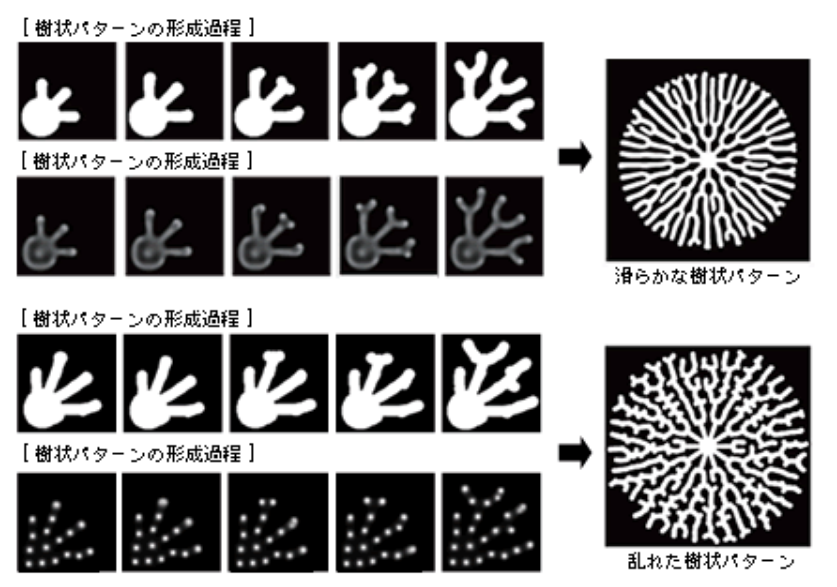
(図9) 条件を変えることで形成されるさまざまな樹状パターン
成長因子と抑制因子の合成速度を変えると、滑らかなパターンや、乱れたパターンがつくられる。
おもしろいことに、乱れたパターンでは、細胞内の成長因子が斑点状に分布しており、分岐した後でもお互いの位置を保とうと動いている。逆に滑らかなパターンは、細胞内の成長因子の分布は連続的で、突起の先端付近で高濃度になっている。この性質が普遍的であるとすれば、神経細胞の樹状突起の外形を観察結果から類型化し、細胞内の成長因子の分布を予測できるかもしれない。
6.物理法則を利用した樹状パターン
実は、神経細胞に限らず、自然界の様々な樹状パターンが、ここまで述べてきた「原理」で統一的に理解できるのである。例えば、最初に紹介したバクテリアコロニーの樹状パターンは、成長因子をバクテリア、抑制因子を培地の栄養分子に置き換えれば、ほぼ同じように説明ができる。その他、雪の結晶や金平糖の突起などもこの原理にしたがうことが、数理的に明らかにされている。
これらの現象を理解するモデルには、共通した特徴がある。つまりいずれの場合にもパターンを構成する領域の成長を抑制(あるいは促進)する拡散性の因子(やそれに相当する状態)が存在し、しかもその因子は領域から供給(あるいは消費)されるのである。この拡散因子の濃度勾配が樹状パターンをつくる主役である。このような性質は様々な現象に普遍的に見られると予想できるので、自然界の樹状パターンの中には、この原理で理解できるものが、まだまだ沢山あるかもしれない。生きものは、このような普遍的な物理法則を利用して、機能的に意味のある空間パターンをつくっているのだろうと考えている。
引用文献
K. Kawasaki et al., J Theor Biol 188, 177 (1997).
R. Kobayashi, Physica D 63, 410 (1993).
J. Wakita et al., Journal of the Physical Society of Japan 63, 1205 (1994).
「非平衡系の秩序と乱れ」沢田 康次 (朝倉書店 (1993/05))
写真提供
杉村薫(京都大学)、上村匡(京都大学)
三浦岳(京都大学)
松下貢(中央大学)※敬称略
望月敦史(もちづき あつし)
1998年九州大学大学院理学研究科博士課程退学、九州大学理学部助手。2002年岡崎国立共同研究機構(2004年より自然科学研究機構)基礎生物学研究所助教授。2007年より同准教授。
![[科学のコンサートホール]BRH JT生命誌研究館](/common/img/logo.svg)

.jpg)
.jpg)