Essay
生き物と数
生き物はなんと美しいのだろう!
そう感じる人は、生き物のどこかに、数学的な美を見ているのかもしれません。
数学が明らかにする真理の世界。その世界を、生き物は、形や生態の中に垣間見せているのです。
フランスの盲目の数学者がこんな話をしてくれた。古代ギリシャ、プラトンのアカデメイアにいた一人の男は、数学でさっぱり学位論文が書けない。あるとき決心して数学が駄目なら生物学でと、生物学で学位が取れる新しい大学を作った。その名はアリストテレス。
この小話にあるように、世間では、数学と生物学は対極に位置する遠い存在だと思われている。学問の性格からすると確かにそうかもしれない。しかし、生物の営みを見ていると、「数学を知っているのでは?」と感じることが多く、数学と生物学は意外に近いものに思える。
北米にいる十七年蝉と十三年蝉は、17年と13年ごとに成虫が地上に現れるので、この2種を揃って見られるのは17×13年=221年ごとということになる。周期が少しだけ違って十八年蝉と十二年蝉だったら、18と12の最小公倍数の36年ごとに揃って出現することになったろう。221年とは大違いだ。おそらく一斉に現れて競合する危険を避けるためにこのようになったのだろうと想像するが、蝉は整数論を知らないはずなのにうまく素数(自分自身と1以外の数では割り切れない自然数)を選んだものだと感心する。もっとも、数学は自然現象の背後にある真理の世界を発見するための学問だから(数学では新しい定理や論理を、発明したと言わずに発見したという。定理や証明はすでに存在していて、まだ知られていないだけだと考えるからだ)、蝉が自然に数学的な行動をしても不思議はないのかもしれないが。
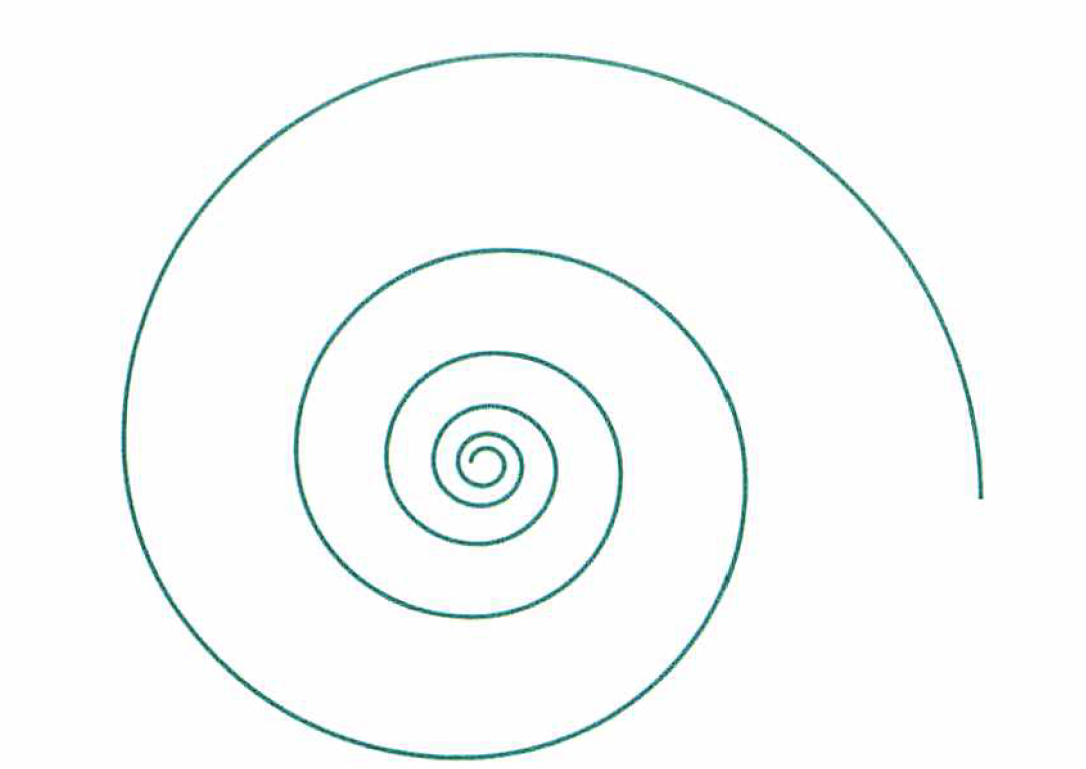
オウム貝の巻き方は、対数螺旋で表される。この螺旋は、極座標(γ,θ)を用いると、r=aeθ(aは定数)と数式化される。直交座標と極座標の関係は(x,y)=(rcosθ,rsinθ)である。
ほかにも面白い例がある。開花植物の葉序(ようじょ)にフィボナッチ数列が現れるのだ。葉は、通常、垂直に伸びた茎の周りを決まった角度おきに螺旋状に取り巻いている。上から見ると、チューリップの葉は2枚で茎を一周するので、1/2×360度ごとに付いていることになる。カヤツリグサ科の葉は、1/3×360度ごとに付いていて、3枚で1周する。サクラやウメでは5枚の葉で2周、つまり2/5×360度ごとに付いている。アブラナ科では3/8×360度、タンポポやグミでは5/13×360度、マツでは数えたことはないけれど8/21×360度だと言われている。ここに出てきた分数の列
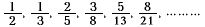
はフィボナッチ数列と関係している。
フィボナッチ数列 { fn } は
f1=1, f2=1, fn=fn-1+fn-2 と表され、
1,1,2,3,5,8,13,21,34,55,89,144 ………
と続いていく。そこで数学者は葉が13/34×360度ごとに付いた植物はあるのだろうかと考えてしまう。
フィボナッチ数列はヒマワリにも現れている。種がきれいな螺旋、それも右回りと左回りの螺旋を描いて並んでおり、その個数は、右回りが55個、左まわりが34個になる場合が多いと聞く。じつはまだ真面目に数えてみたことはないので、今年の夏は数えてみたいと思う。品種改良して、それぞれ144個、89個の螺旋をもつ巨大なヒマワリ、さらに多くの螺旋をもつヒマワリもあると聞いている。それにしても不思議なのは、ここに出てくる数はすべて隣り合うフィボナッチ数だということだ。これも葉序と同じ原理で説明できるのだろうか。

ヒマワリの種は螺旋を描いて並んでいる。右巻き螺旋の数が55個なら左巻きは34個に、144個なら89個になることが多いという。
(図=Scientific American 1969/3をもとに作成)
私たちが十進法を使うのは両手で10本の指があるからで、天与のものと思われる数学も、私たちの生物としての存在に大きく影響を受けている。ではなぜ指は5本ずつあるのか。理由を知りたいが、こうした問いかけは現代科学では禁じられているのかもしれない。アリストテレスの目的因の考察を忘れて、変化のプロセスだけを記述することで大成功を収めた近代科学は、指はなぜ5本あるのかと問うことはやめにして、5本の指ができるプロセスを記述してきた。だから、葉序やヒマワリがフィボナッチ数と関係していたり、オウム貝の曲線が対数螺旋になっている理由を問うのは、科学を逸脱することになるのかもしれない。でもやはり私は理由が知りたい。
整数や素数の概念は、知的生物に普遍のものとして、アメリカでは異星人に素数を含むメッセージを送ったが、そもそも彼らが十進法を使っているかどうか、数の概念をどのようなものとしてもっているか、数に関心をもつものとして興味がある。
近代数学の成功の原因は、数を自由に扱う方法だけでなく、関数の概念を獲得し、時々刻々と変化する量を記述可能にしたことにある。数とは根本的に違う関数の概念を理解する異星人はいるのだろうか。
上野健爾(うえの・けんじ)
1945年熊本県生まれ。東京大学理学研究科博士過程修了後、同大学助手、京都大学理学部講師、助教授、教授を経て96年より同大学理学研究科数学教室教授。理学博士。複素多様体論を専門とし、著書に『デカルトの精神と代数幾何(増補版)』(共著、日本評論社)などがある。
![[科学のコンサートホール]BRH JT生命誌研究館](/common/img/logo.svg)

.jpg)
.jpg)