LECTURE & TALK
生命科学から味わう謎解きの楽しさ
LECTURE & TALK
生命科学から味わう謎解きの楽しさ講演
CHAPTER

1.はじめに
生命科学は謎を解いているという感覚が好きでやっていました。パズル、ミステリーなどは謎があるから楽しい。謎解きは楽しむための重要な要素です。サイエンスもその謎解きの範疇で語れるのではないでしょうか。
なぜ謎解きは楽しいのでしょう?謎を解くために頭を悩ませ、あるとき閃いて謎が解けるとすっきりする。この悩んで解決する過程が楽しいわけです。ではどんな謎が魅力的だと思いますか?
人類史上最も魅力的で最も人を不幸にしたパズルは『フェルマーの最終定理』だと思います。1637年ごろにフェルマーが考案し、証明されたのは約360年後。その間この問題に取り組んで結局解けなかった、人生を棒に振った数学者は約5万人いると言われています。
誰にも解けなかった謎というのは魅力的ですよね。でも難し過ぎて人生を棒に振るのは嫌だし、そうでなくとも難し過ぎて解けなかったら腹が立ったりもします。
簡単過ぎても解き甲斐がない。そこで僕は生命科学をおすすめします。

2.生命現象のほとんどは「謎」
一つの例として、抗体遺伝子の話を紹介します。
人の体には日夜いろんな病原菌、異物が侵入してきます。それに対して、人間の体は抗体を作ります。新しい病原菌が入ってきたら新しくそれにピッタリ合う抗体を作る必要がある。この抗体というのは遺伝子から作られます。でも、遺伝子の数は全部で2万個ほど。なのに、そこから何億通りもの抗体を作ることができます。
どんな抗体が必要になるかわからないし、未知のウイルスもあるはずなのに、我々の体はちゃんと対応できる。それはなぜなのか、長年科学者たちの頭を悩ませた大きな謎でした。
実は、抗体を作る遺伝子の一部が、一つの完成した塊ではなく、バラバラに分かれた状態になっていて、それらを組み合わせると約1万個のパターンの抗体遺伝子を作ることができます。抗体は抗体遺伝子を2個組み合わせて作るので、1万×1万で1億個のパターンを作り出すことができるのです。
これは長年の謎が、構造一つですっきり解かれたわけで、みんな度肝を抜かれました。ちなみに、解明した研究者はノーベル賞を取りました。
このように綺麗に謎が解けると非常に楽しいわけです。
でも、ほとんどの科学本やセミナーでは、謎や疑問とそれに対する答えしかわからず、肝心の「謎解きの仮定」が説明されないので、科学者が味わっている楽しさを味わえないんですよね。今回の講演では、その楽しい謎解きの過程の部分を強調して話していきます。みなさん楽しんで聞いていただければ幸いです。
3.貝の形
貝にはいろんな種類があります。形は様々あるのに、とても規則的で、どこか共通性がありそうですよね。どうすればこんな形が作れるのか、どうしてこの形なのか、見ただけではわからない。これからご紹介する「どうして貝はこんな形が作れるのか?」というお話は、僕ではなく主に愛媛大学の岡本隆先生が行われた研究です。
まず、貝殻の成分の性質を考える必要があります。
貝殻は炭酸カルシウムという、硬くて変形しない性質のものでできています。この硬い殻は体の防御のために必要です。
でも、硬い構造だと貝にとって困ることがあります。それは体が成長した時です。
人間などの脊椎動物は、体の成長に合わせて骨を大きくします。骨は内側を削って外側を足していくという技が使えます。内側に骨を削る細胞と、外側に骨を足す細胞があるからです。
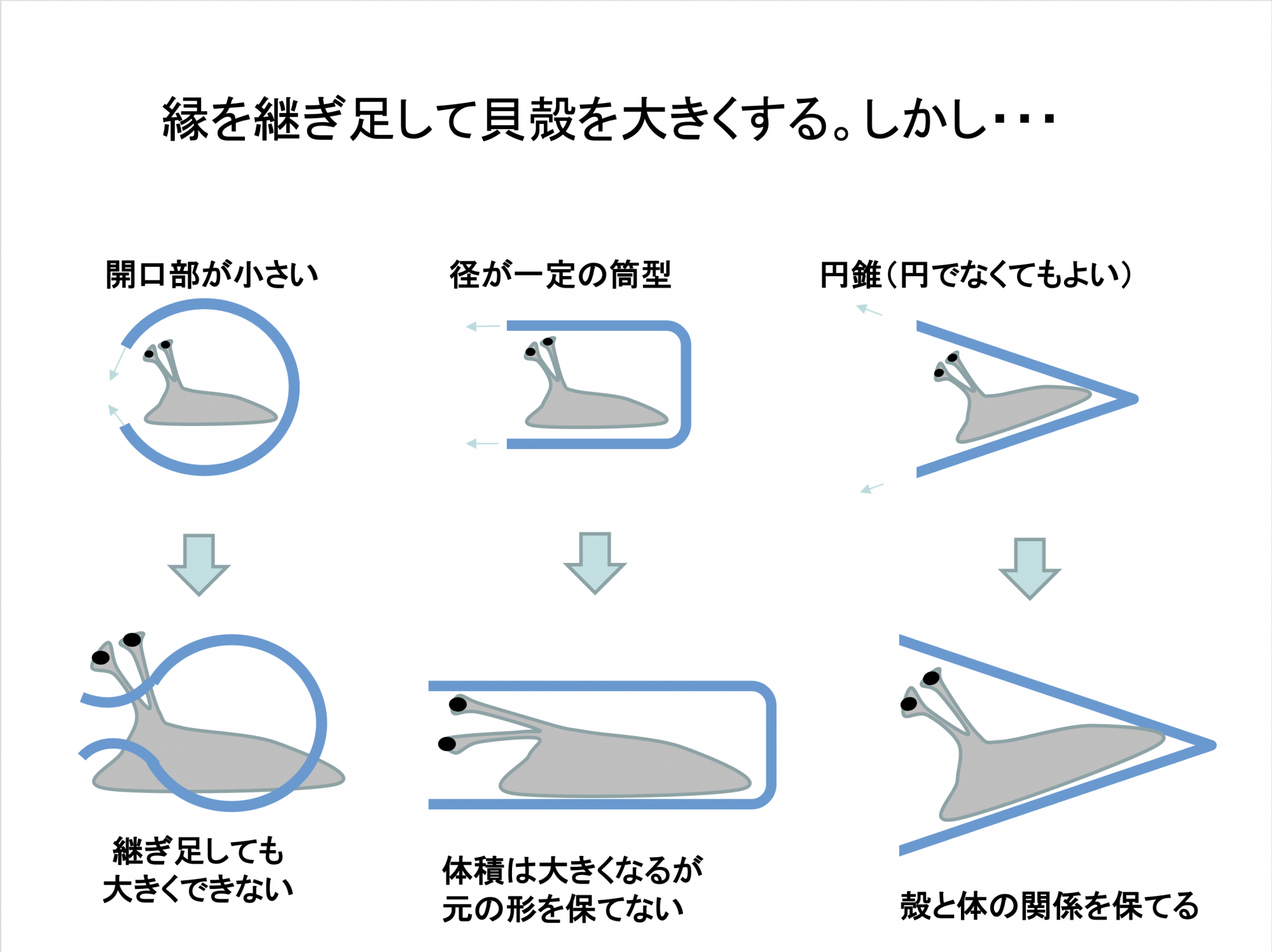
では貝ではどうかというと、骨とは違って貝殻の外側に細胞が存在しません。内側に足したらどんどん窮屈になってしまう。これでは困ってしまいますね。
この図の青い部分が貝殻で、赤い部分が細胞のある部分です。殻を足そうと思ったらこの破線で囲んだ部分にしかできません。だからフチを伸ばすという方法で解決しました。

でも、ただフチを伸ばすだけではうまくいきません。軟体動物といえど体の形は変えずに大きくなりたいのです。でも形によっては、フチを伸ばした場合殻の形の縦横比が変わってしまう、つまり体の比率も変わってしまう。どんな形なら都合がいいでしょうか?
それは円錐のような形なのです。
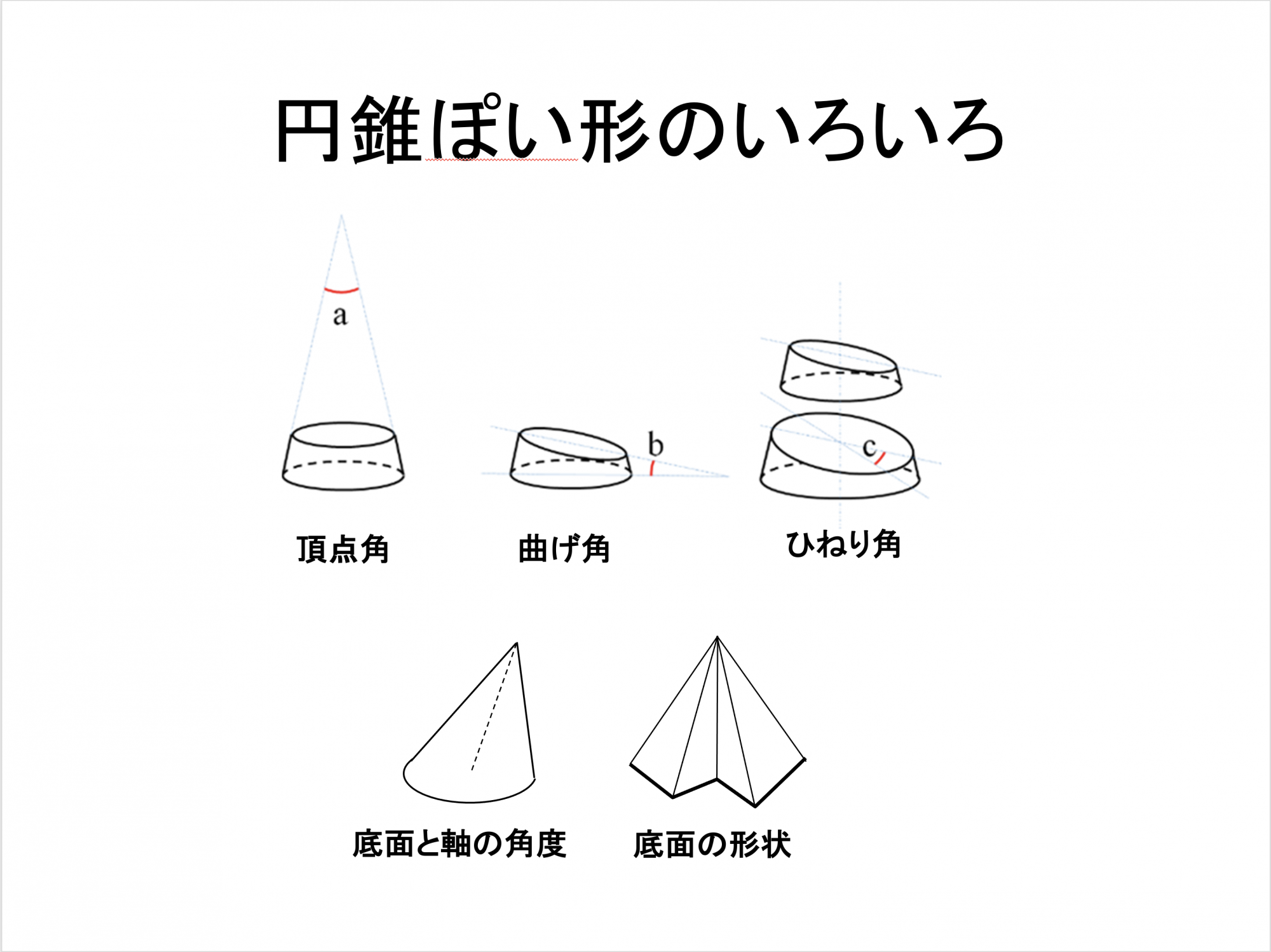
貝の基本形は円錐です。でも世の中にはいろんな形の貝殻がありますよね。円錐を基本形に、バリエーションを出すためにはどうしたら良いのか。
フチを伸ばすときに、たくさん伸ばす部分とちょっとしか伸ばさない部分を作る。すると少し傾きます。さらに、伸びる角度を少し捻ることもできます。他にも軸の角度を変えたり、底面の形状を変えることもできます。ここは頭の中で考えるのは難しい部分ですね。でもこの5つが円錐っぽい形で体の形を変えずに大きくできる変異のパターンです。
これを組み合わせるとどんな形ができるのでしょうか。それを計算して数理モデルを作ったのが岡本先生です。その数理モデルを基にシミュレーターを作りました。先ほど紹介した5つのパラメーターを変化させることで、このようにあらゆる貝殻の形を再現できるものです。



このシミュレーターは誰でも自由に使うことができるので、ぜひパラメーターをいじって遊んでみてください。
https://keisukemazdagithub.netlify.app/
-講演の記録動画では、近藤先生が様々な貝の形を再現する実演をご覧いただけます。-
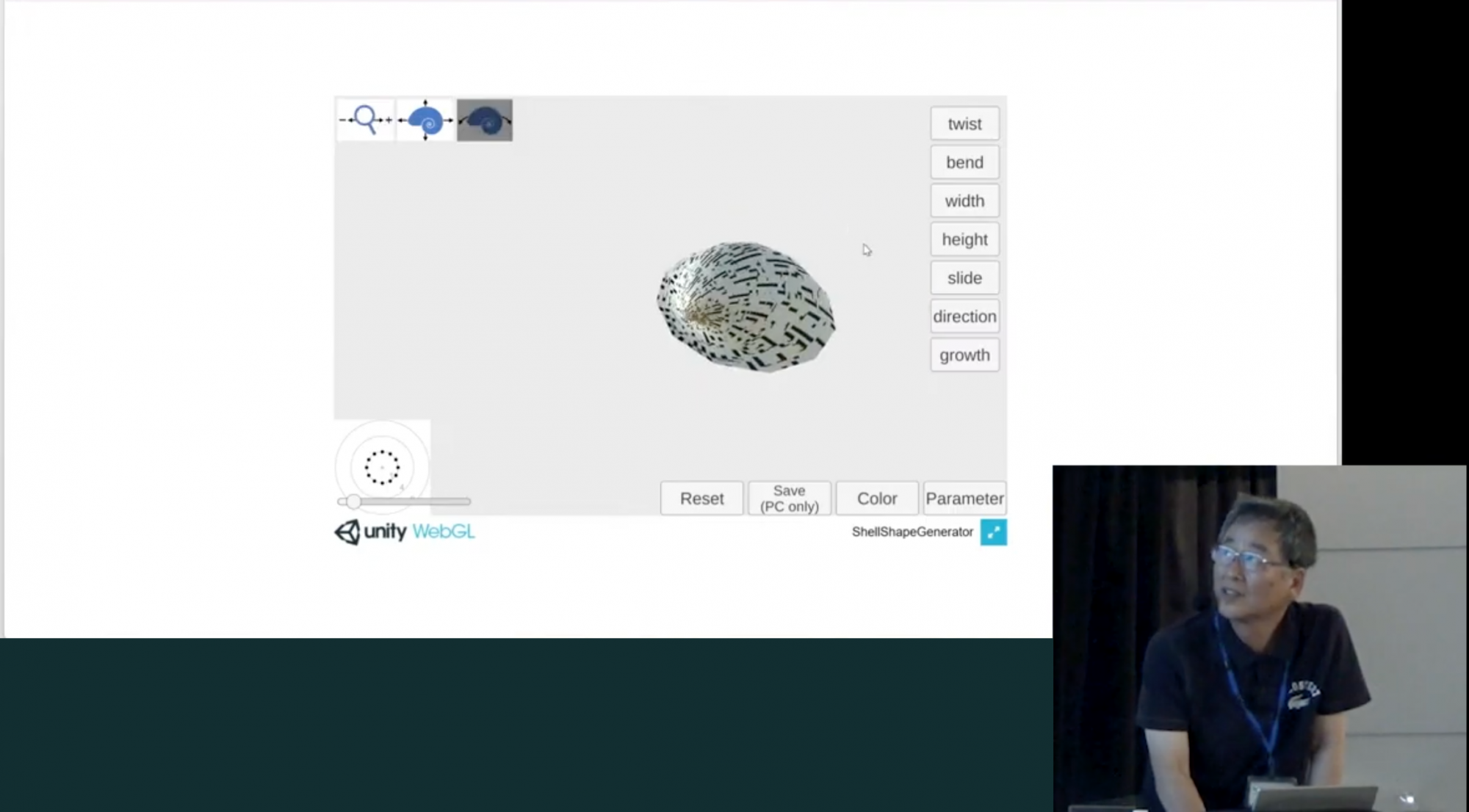
どうでしょうか。ハマグリっぽい形になりましたね。
このシミュレーターの凄いところは、巻貝はもちろん、二枚貝も作れるところです。みなさんは二枚貝と巻貝は全然違う形だと思っていたのではないでしょうか。実は体の形を変えずに成長するには5つのパラメーターしかいじれなくて、どの貝にも共通している、というのがこのシミュレーターでわかってもらえたと思います。なかなかすっきりしませんか?
僕が初めてこれを聞いた時は本当にびっくりしました。
さて、これでほとんどの貝は説明できたように思えます。では、サザエのような突起のある貝はどのようになっているのでしょうか。
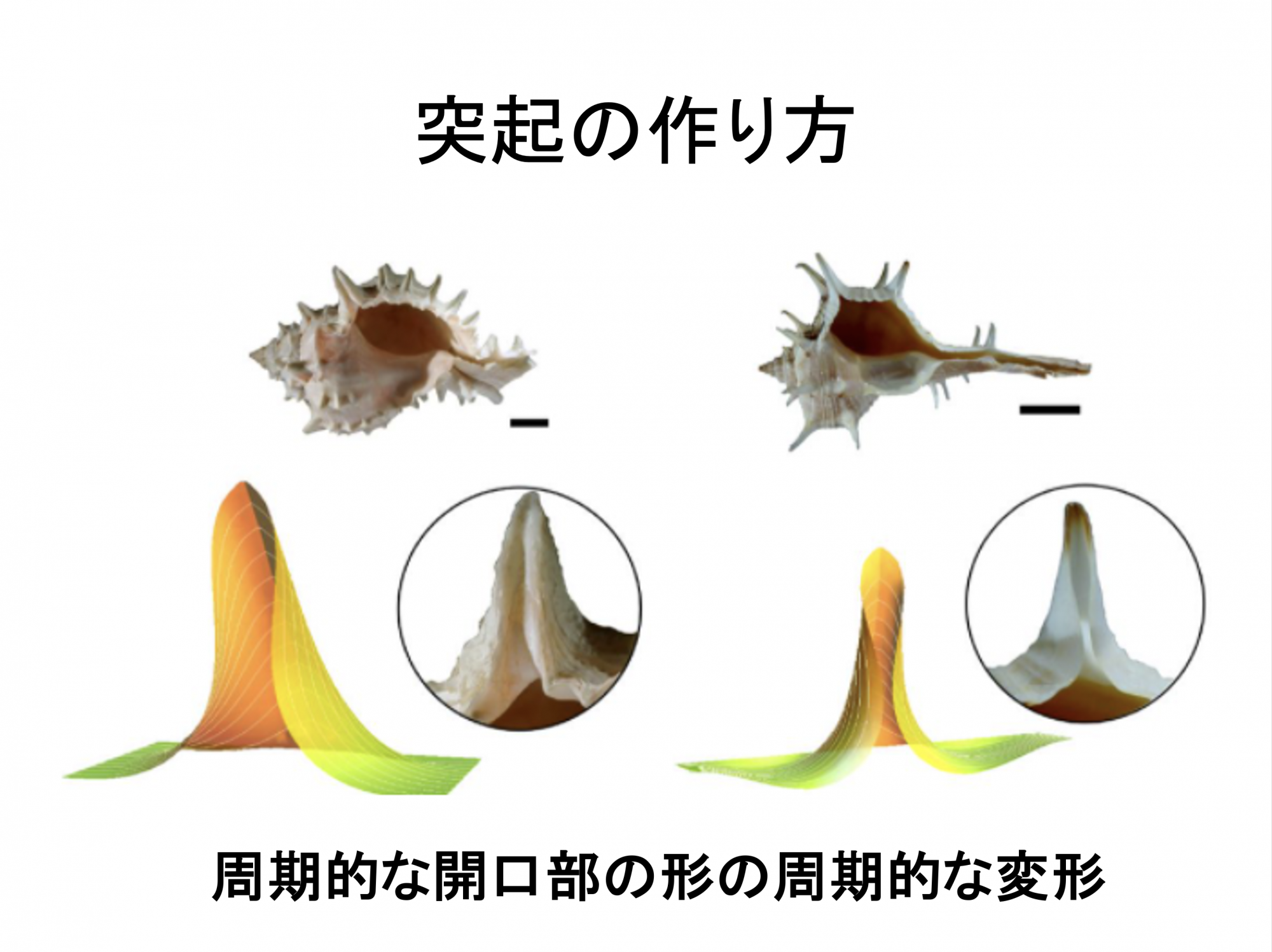

実は成長するときに、一瞬だけフチの一部をピュンと変えているんですね。
いつもは丸い開口部を、たまに尖らせる、それを周期的に行うということで説明できます。
それでは、一度わかったことをまとめましょう。
貝殻の材質は硬いカルシウムの結晶でできています。それは物理的な制約のため、形態は錐体を基にして、そこから貝は5つのパラメーターをいじることができます。どの貝もそのルールの中で殻を作っているので、1つの数理モデルで再現が可能、ということです。
4.貝殻はどうしてこの形?
二枚貝は砂の中に潜って生活しているので、砂が入り込まないようにピッタリ蓋をしているわけです。カサガイは、岩に張り付いて生活しているので弱点である体がはみ出ないようになっています。巻貝と違ってひねりのない平面的な殻を持つオウムガイ。あの独特な形は海を自由に泳ぎ回る浮遊生活をするのに適しています。
では、サザエのような巻貝はなぜ、ひねりが必要なのでしょうか?
それは、見比べてみると一目瞭然です。
巻貝というのは海の底や岩場にくっついて生活しています。オウムガイの殻を机に置いてみると、どう工夫しても必ず殻と机の間に隙間ができてしまいます。貝殻というのは外敵から身を守るために必要なものなので、隙間があると困るわけです。オウムガイ自身は泳いで逃げられるから困りません。でも這って進む貝は足が遅いので襲われてしまったら逃げられない。
ではどうすればいいのか?
貝殻をひねればいいのです。
オウムガイと巻き貝を比べると、巻貝は開口部が見事にピッタリと地面にくっつく形になっているのがわかります。

でもひねると困ることもあります。
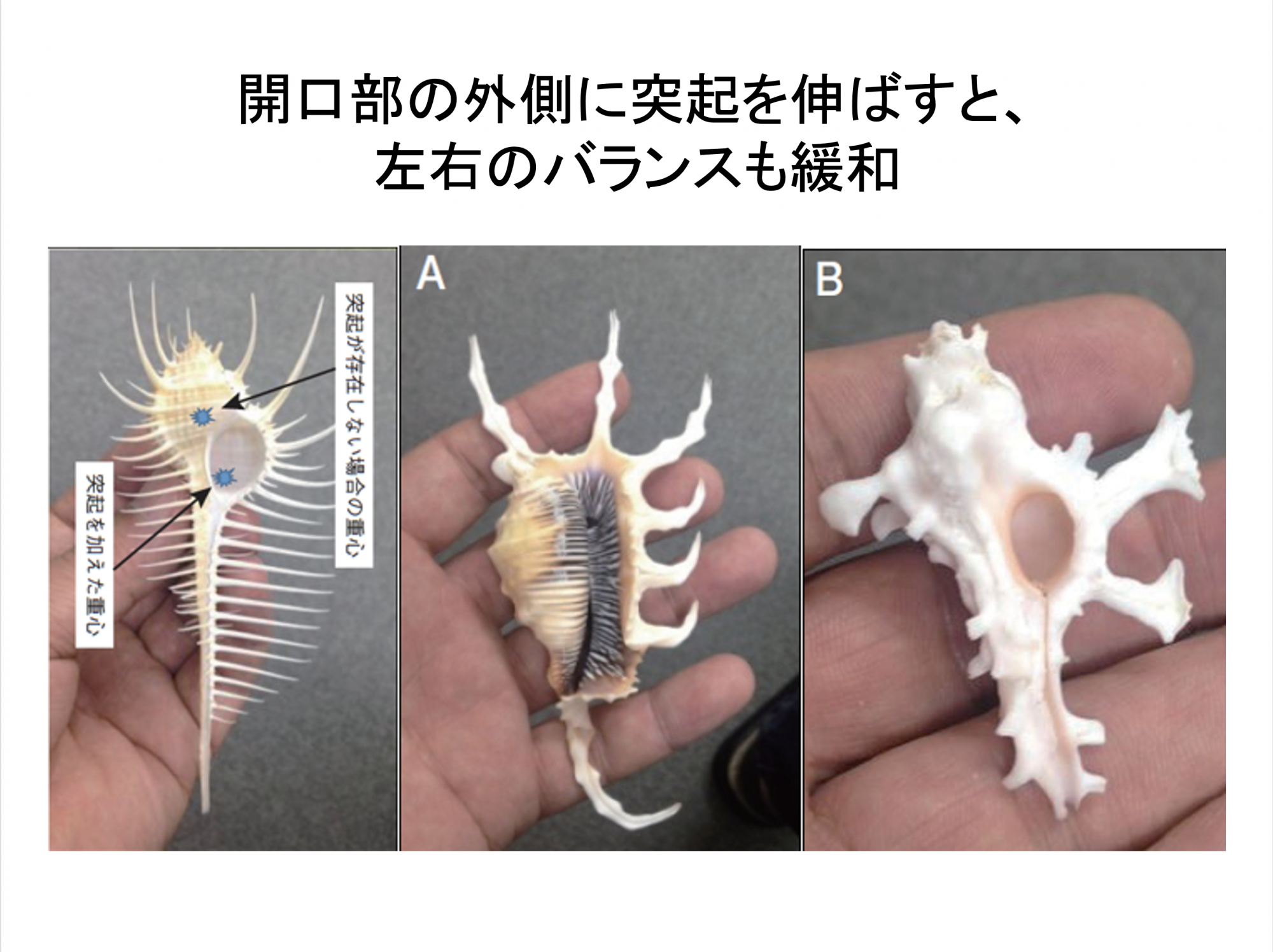
貝殻の形が左右非対称になってしまう。そうすると重心がズレるわけです。

こういった貝の場合、移動するときは貝殻を持ち上げて歩くわけですが、貝殻の重心が前後にも左右にもズレています。これがどういうことかというと、片側だけめちゃくちゃ重いランドセルを背負うような感じです。それではバランスが悪いし背負いにくいと思いませんか?ではどうすればいいのでしょう。
やじろべえみたいに重さでバランスが取れたらいいのです。貝殻の重心が真ん中に来るようにするために、あのトゲがあるわけなんですね。
では次に、どうやってトゲを作っているのか、見てみましょう。
殻を作っているのは外套膜(がいとうまく)という部分です。ホタテガイで言うとヒモの部分です。珍味として食べますよね。ここは筋肉で、貝が自分の意思で自由にぐにゃぐにゃ動かせるのです。だから人で言うと手で粘土をこねて陶器を作るようなものだと言えると思います。
面白い例をご紹介します。カジトリグルマとクマサカガイです。似たようなトゲのあるシルエットですが、クマサカガイの方はただのトゲではなく、別の小さな貝がくっついています。

これは人工的に作られたものではありません。クマサカガイ自身が周りに落ちている手頃な貝殻を使って、角度を調整してくっつけているんです。
結合部分をみると、非常に見事にくっついているので、これが人の手による物ではないことがわかります。
面白いことに、カジトリグルマとクマサカガイは近縁種なんです。クマカサガイがどう考えても意図的にトゲを作り出しているので、トゲを作る方法は違えどカジトリグルマも意図的にトゲを伸ばしていると考えて良さそうです。
貝殻のトゲが意図的に作られたことはわかりましたが、ではひねりについてはどうでしょうか?
みなさんは、異常巻きアンモナイトというアンモナイトはご存知でしょうか?アンモナイトというと、ひねりのない貝殻を持つものが一般的ですが、異常巻きアンモナイトはこんがらがったような貝殻を持ちます。あまりにも複雑な形なので、見つかった当初はただぐちゃぐちゃに巻かれているのだと思われていました。しかしその後、何個も同じ形の貝殻が見つかったので、これはちゃんと規則性があるということがわかりました。そのルールを調べてみるとひねりの規則性が見えてきました。右にひねって、左にひねって、また右にひねって……これを交互に繰り返しながら巻いていくと、正確にあの形になります。そして、そのひねりを行ったことで、海中を泳ぐ時に体の水平のバランスがうまくキープできるのです。ここから体の成長に合わせてひねりのパラメーターをいじっているということがわかりました。この研究も岡本隆先生によるものです。
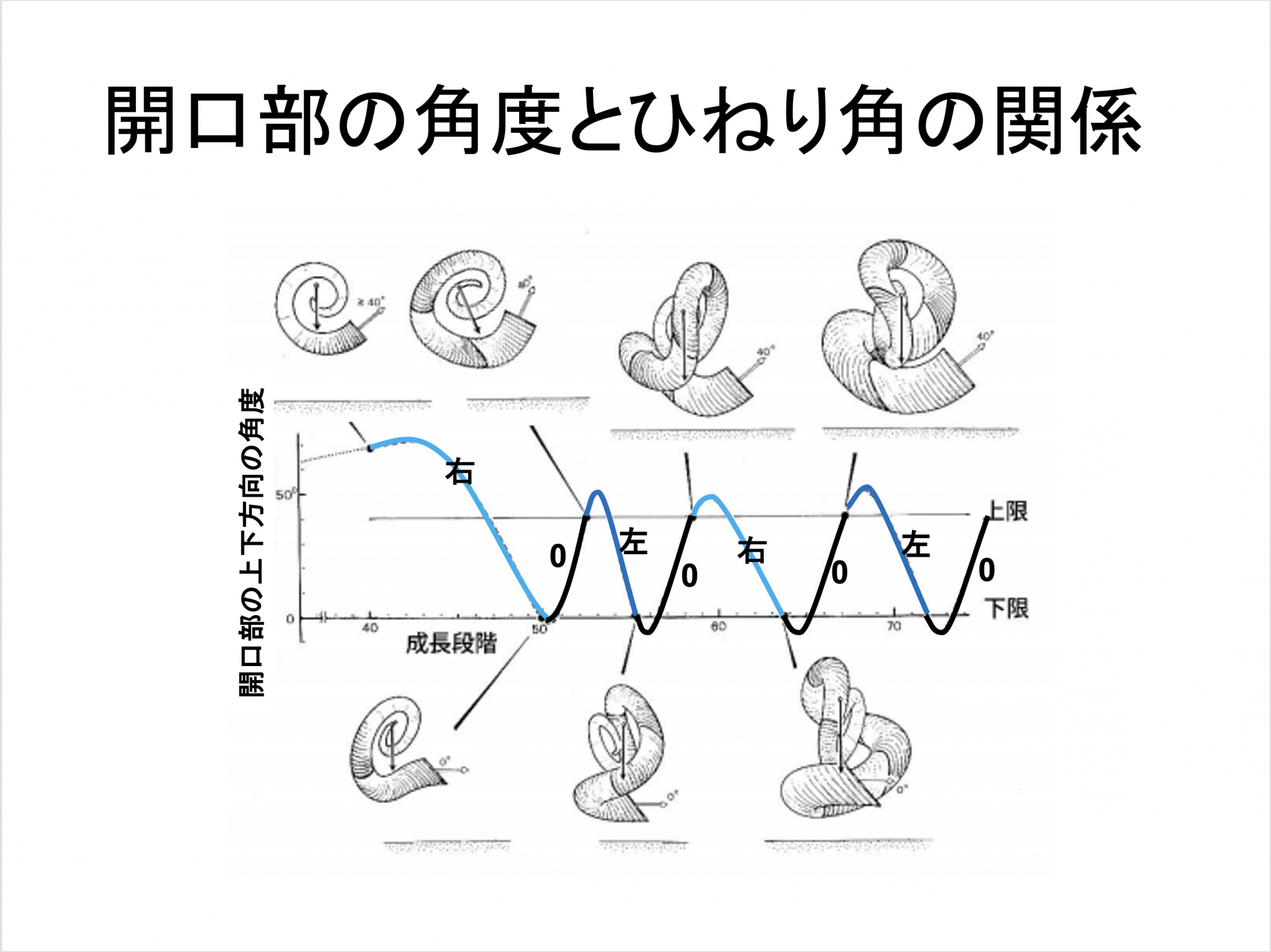
Okamoto, T. (1988) Developmental regulation and morphological saltation in the heteromorph ammonite Nipponites. Paleobiology 14: 272–286.
アンモナイトは絶滅してしまいましたが、現代にも面白いひねり方をする貝は存在しています。
ここからわかることは、成長に合わせてそのつど貝自身が調整してトゲを伸ばしたりひねったりしているということです。遺伝子情報に組み込まれていて自動的に成長しているわけでは無いのです。
ということで、それを証明するための実験を行いました。
正常な貝に無理やりサンゴをくっつけて、強制的に殻の重心をずらしました。バランスを崩した貝の多くは死んでしまいましたが、一部生き残ったものもいます。
それらの貝殻を観察してみると、巻きが上向きになっていたり、下向きになっていたり、変な角度になっていました。まだデータが少ししか無いので、結果は出せませんが、やはり意図して貝殻を形成していそうですよね。


結論。貝殻の形は、明確な意思を持って外套膜が作る、手作業の工作物。貝殻の形を決めるのは、個体のバランス。というお話でした。
5.熱帯魚の模様
熱帯魚は派手な模様を持つイメージがありますよね。近縁種の魚でそれぞれ違った派手な模様を持っていても、体の構造を見てみると骨の形や内臓などの体の仕組みにはあまり差がなく、大体同じようなものです。

だから模様というのは皮膚の上で勝手に現れるものだと推測できます。さらに、模様に注目してみると様々な模様がありますが、これは点や線などの等間隔の並びであることに気が付きませんか?
等間隔のパターンが自然にできる現象。生きものから離れて考えてみると、身近にたくさんあります。それは「波」です。

こうして並べてみると、そっくりですよね。だから模様も体の中で波のような現象が起きているのかもしれない、という仮説です。この仮説はアラン・チューリングという天才数学者が約70年前に書いた難しい論文によるものです。二種類の化学分子が互いに干渉しながら作ったり壊したりする時、ある条件下で波ができると、チューリングは考えました。この反応による波のことを、「チューリング波」と言います。
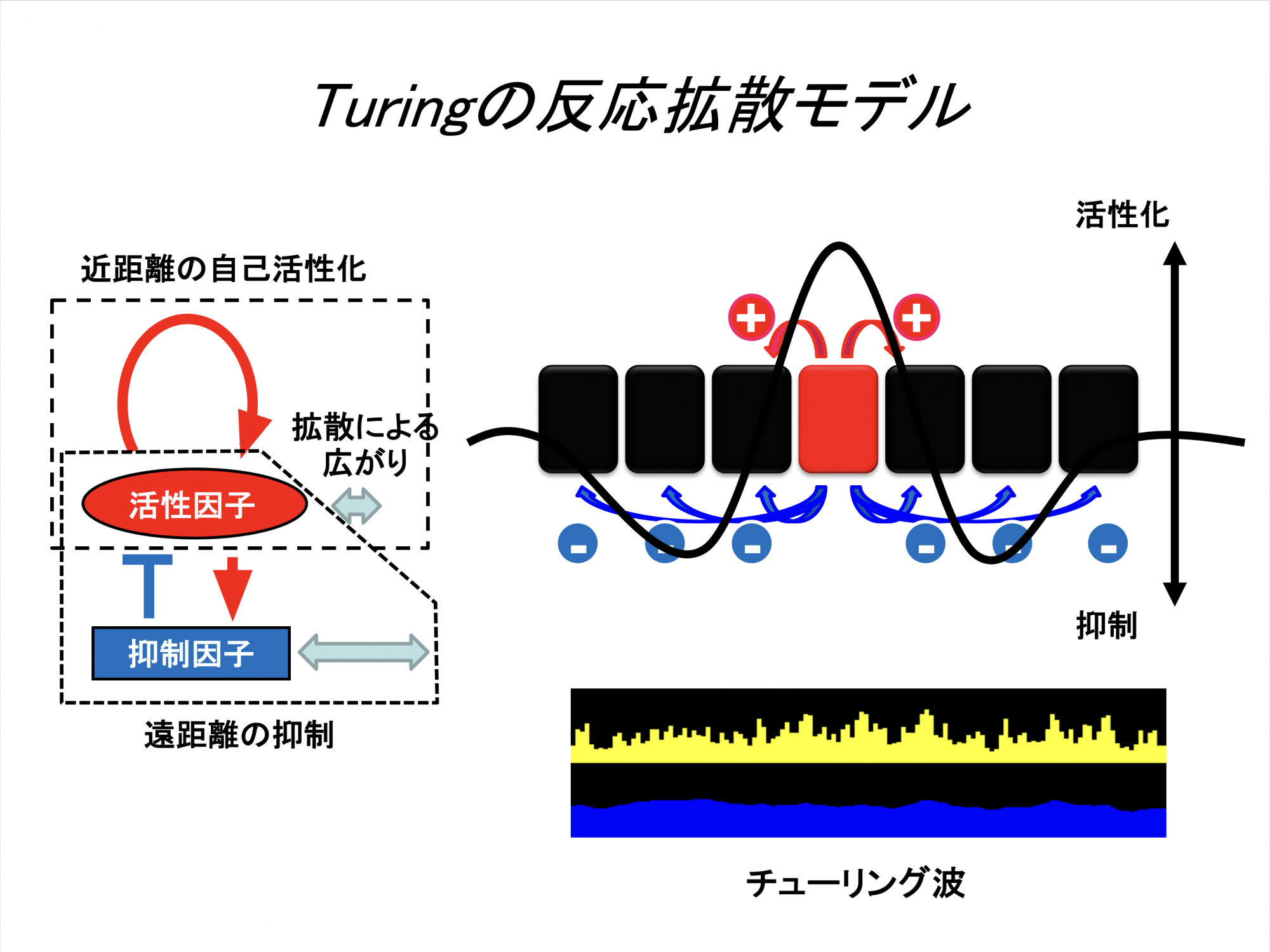
チューリングが考えた数理モデル「反応拡散モデル」からシミュレーションを作ってみました。試しに動かしてみると面白いことに、何も無いところから動物の模様ができます。模様を壊しても自然と治るし、いろいろなパターンを作ることもできます。
-講演の記録動画では、近藤先生が様々な模様を再現する実演をご覧いただけます。-



このシミュレーターも誰でも自由に使うことができるので、ぜひ遊んでみてください。
https://www.fbs.osaka-u.ac.jp/labs/skondo/simulators/rd_new.html
と、いうわけで、このチューリングの理論を使うと、我々が知っているすべての動物の模様が再現できます。先ほどお見せした貝殻のように、一つの原理ですべての説明ができる。とても興味深いですよね。
しかし、チューリングが発表した当時は生物学者のほとんどがこの理論を信じませんでした。
なぜなら、「体の中に波ができる」という聞いたことのないアイデアで、シミュレーションのみ。誰も実験で証明していない、つまり証拠が無いので疑われてしまったのです。
僕としてはあまりに美しくて楽しかったので、証明したくなりました。
じゃあどうしたら証明になるのだろう?どうしたら信じてもらえるのだろう?と考えました。波というのは動きですよね。水があれば波になるわけではなく、水の表面が動くから波になる。だから「動き」を見つけたらいいのではないかと思いました。
タテジマキンチャクダイという魚の模様を見ているうちに、模様の変化に気がつきました。小さい時には縞模様に枝分かれがあるけれど、大人になると無くなります。それに気がついた時に「あ、やっぱり模様は動いているな」と思いました。
縞模様の間隔を変えずに縞の数を増やしている。波とは等間隔を刻むことなので、やはり関係がありそうです。
シミュレーションしてみると、まるでジッパーが開くような動きで枝分かれの分岐点がスライドし、一本の線が二本に分かれました。タテジマキンチャクダイを育てて観察すると、まさにシミュレーションの通り、枝分かれが動いていきました!僕の生涯で最も美しい実験結果だと思います。この実験によって、無事チューリングの理論を実証することができました。

このシミュレーターは模様の予測もできます。縞模様の一部の縞を繋がらないように操作すると、下の縞が上に引っ張られると予測されました。実際にゼブラフィッシュという魚で実験してみると、予想されていた通りの模様になりました。

また、シミュレーションによって、暗い斑点と明るい斑点は中間に迷路模様を挟んでこのようにグラデーションしていることがわかりました。それが本当なのか、同じ魚で模様が暗い斑点のものと明るい斑点のものを掛け合わせてみると、予測通りに迷路模様の子供が産まれました。

このように、ありとあらゆる模様の予測ができましたが、その後は15年ほどかけて様々な実験を泥臭く行いました。僕のところのラボメンバーに力を尽くしてもらって、最終的に模様を作る分子的な原理の発見に至りました。そのおかげでゼブラフィッシュの黄色と黒色の色素細胞がチューリングの言っていた分子の波を生む関係と一致していることが解明できました。
チューリングの理論によって説明できる模様なら、自由に動物の模様を変化させることも理論上可能なので、やってみました。左上(wild type)が本来のゼブラフィッシュの模様です。それをこのように斑点模様やヒョウ柄など様々な模様に変化させることができました。

現在は非常に多くの学者がチューリングの理論を認めています。
例えば、マウスの指を使った実験。従来、指は一本いっぽん個別に作られていると考えられていました。しかし、手ができる範囲を大きくするとなぜか指の数が増えることがわかりました。これは従来の考え方では説明できなかったのですが、「波ができる範囲が広がったから指の数が増えた」とすれば説明がつきます。つまり指の形成は波によって引き起こされていたのです。そのほかにも鳥の羽根ができる間隔が等間隔であることも波の理論だし、指の関節の間隔も波だし、脊椎が等間隔なのも波。指紋だって波。今の発生学者のほとんどは体の中に見つかる等間隔の構造は全部波によるものだと考えています。
結論。模様は波が作ると考えると、すべての種類の模様を同じ原理で説明することができる。観察してみると、魚の模様はシミュレーションの通りに変形し、模様の予測もできる。実験してみると、ゼブラフィッシュの模様を自在に変えることができました。
パズルを解いたような快感がありましたが、実験がこんなにうまくいくことはそうそう無いです。たまたまうまく行ったのだと思います。
これまでに研究を一緒に行なってくださった皆様には心より感謝しております。
ご清聴ありがとうございました。

1959年東京都生まれ。1982年東京大学理学部を卒業。1988年京都大学大学院 医学研究科博士課程修了。2001年理化学研究所発生・再生科学総合研究センター チームリーダー。2003年名古屋大学大学院理学研究科生命理学専攻教授。2008年大阪大学大学院 生命機能研究科教授を経て、2024年に国立遺伝学研究所 所長就任。主書に『波紋と螺旋とフィボナッチ』(学研メディカル秀潤社)


![[科学のコンサートホール]BRH JT生命誌研究館](/common/img/logo.svg)


.jpg)
.jpg)